Research
1. Computational fluid dynamics and machine learning for Flow control
Flow control is a process of manipulating the flow to achieve desirable aerodynamic performance. The flow control technique in this work is inspired from covert feathers in birds—a set of self-actuating feathers located on the suction surface of the wings. During unsteady flow separation, these feathers protrude into the flow and provide lift enhancements, for reasons that are still not understood. We study the utility of covert feathers as a both passive and active flow control technique.
Passive flow control
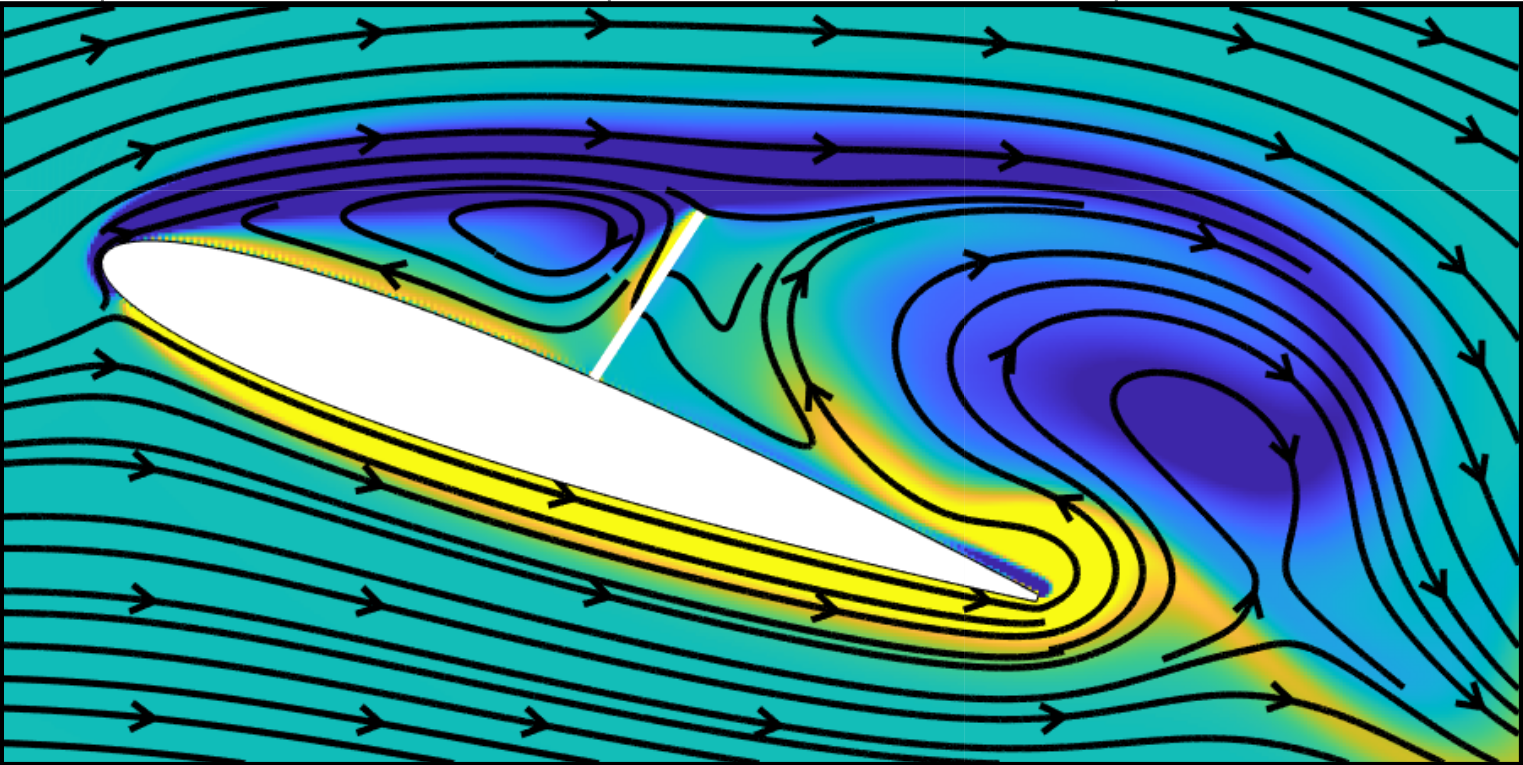
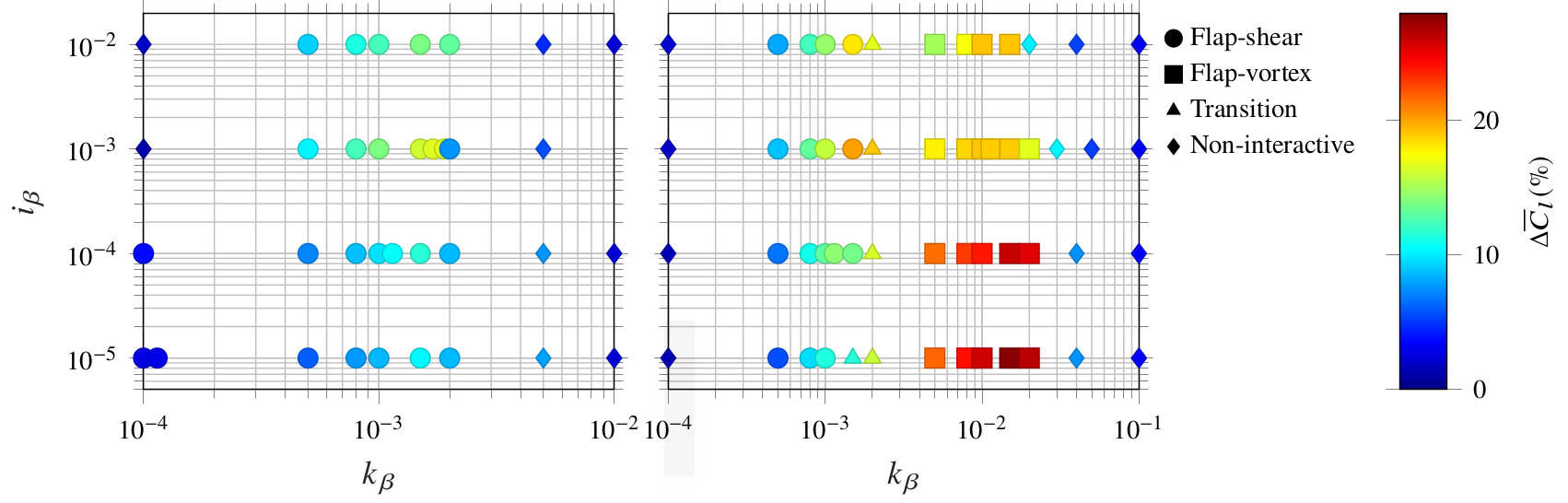
We numerically investigated a model system in which a passively deployable, torsionally hinged flap is mounted on the suction surface of a stationary airfoil via high-fidelity nonlinear simulations as shown in the figure below. A parametric study performed by varying several flap parameters yielded lift improvements as high as 27% relative to the baseline flap-less case. A k-means clustering algorithm with carefully chosen inputs revealed two dominant flow behavioral regimes responsible for these lift improvements. More details about this work can be found [here] and [here]. We also analyzed a system of multiple torsionally hinged flaps on an airfoil, details of which can be found [here]. We have also collaborated with Prof. Aimy Wissa’s group to compare our numerical results with their wind-tunnel experiments, the link for which will be updated soon.
Active flow control using reinforcement learning
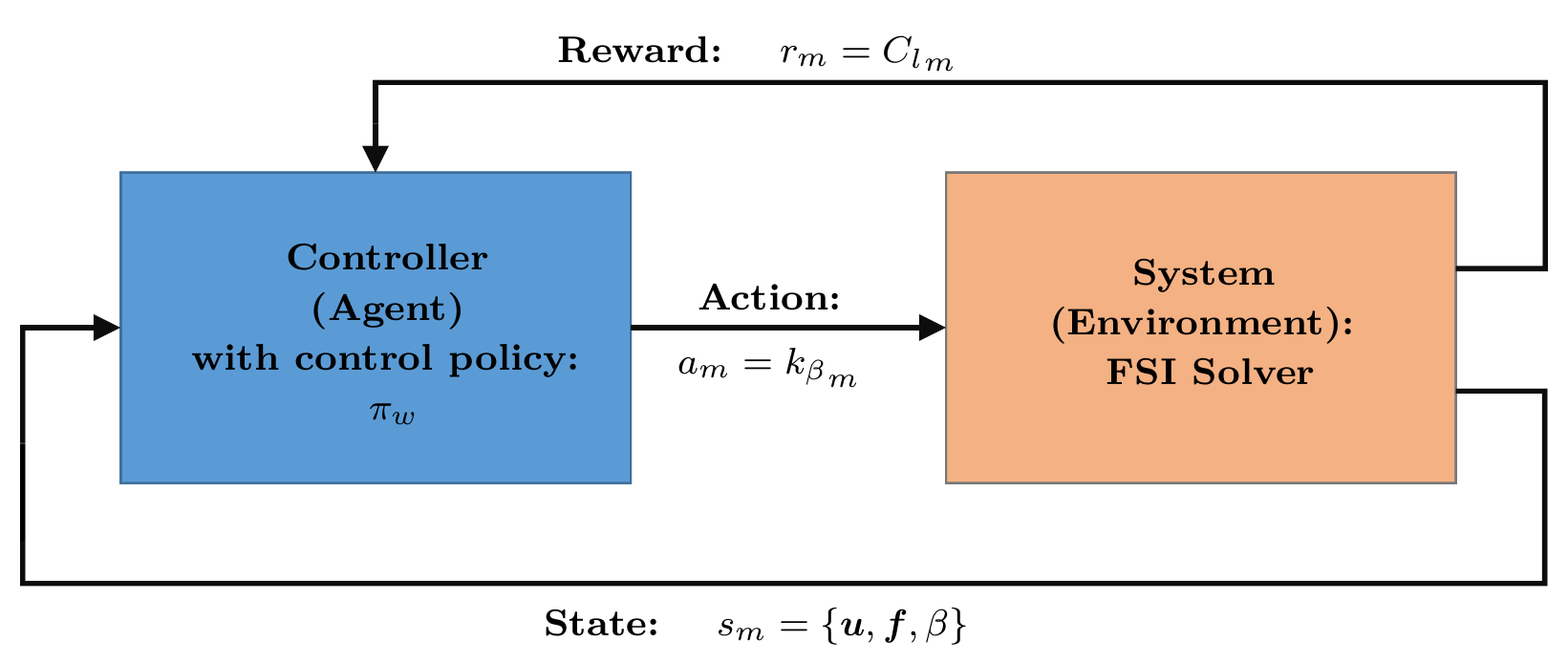
We are currently designing an active flow control counterpart of the above-mentioned passive flow control strategy for further augmenting the airfoil lift. Using reinforcement learning, we are developing a closed-loop feedback controller for actuating the hinge stiffness as shown in the figure below. The controller is constructed to maximize reward or aerodynamic lift under unsteady gust conditions. A neural network architecture is used to construct the controller/agent which takes the flow-state of the system as the input and outputs the instantaneous value of stiffness. PPO, a policy gradient optimization algorithm is used to train the agent. The results will be updated soon.
2. State estimation using deep learning
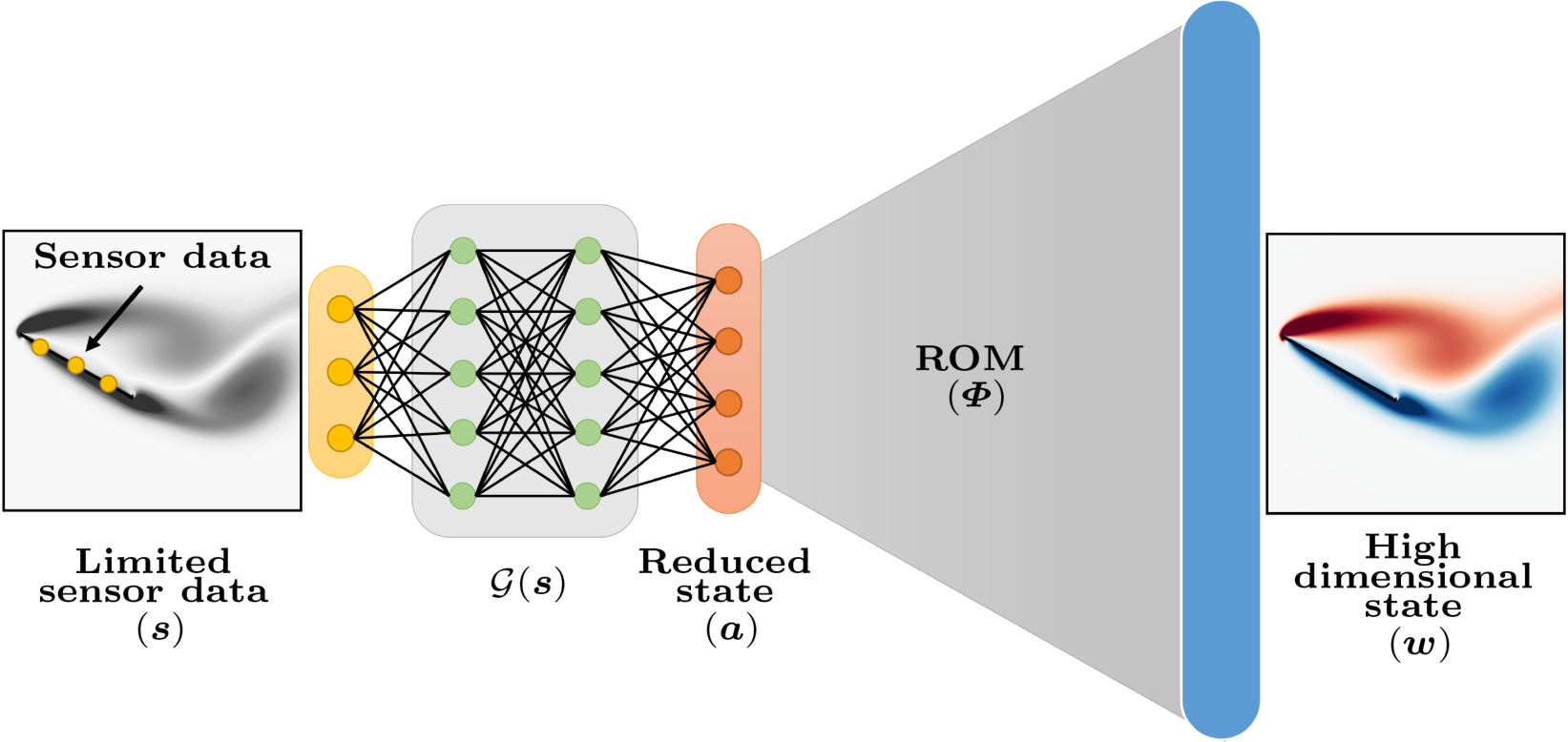
In this work, we have developed an nonlinear state estimation methodology for dynamical systems where real-time sensor data is used to estimate the full state of the system. In this method, first, a reduced-order model (ROM) is constructed and associated reduced states are evaluated. Then, the sensor data is mapped to the reduced states using a deep neural network architecture consisting of fully connected layers. This method was successfully demonstrated in estimating the full flow-field around a flat plate at a large angle of attack, where the ROM was built using principal component analysis (PCA) a.k.a. proper orthogonal decomposition (POD). More details about this work can be found [here].
3. High performance computing and development of efficient algorithms
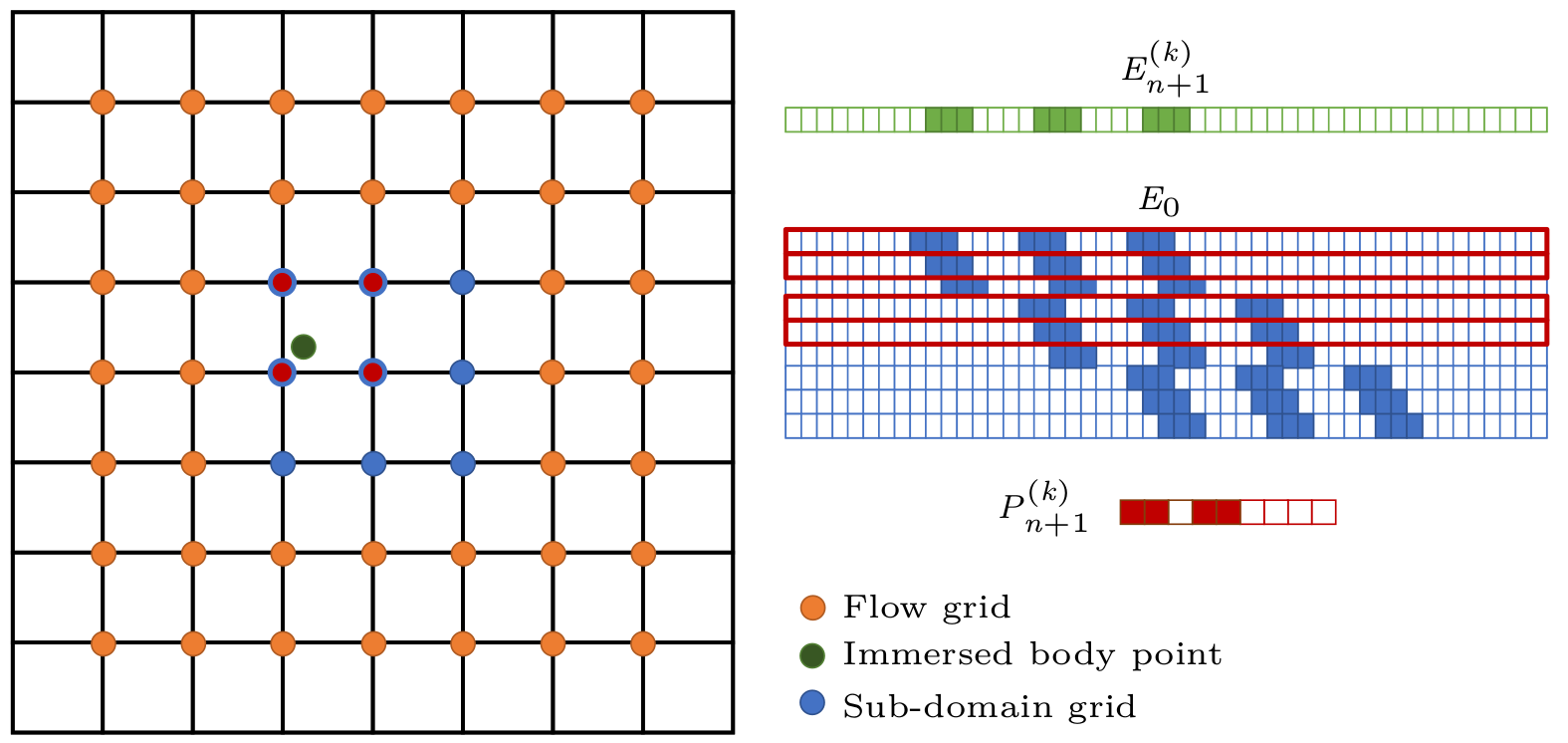
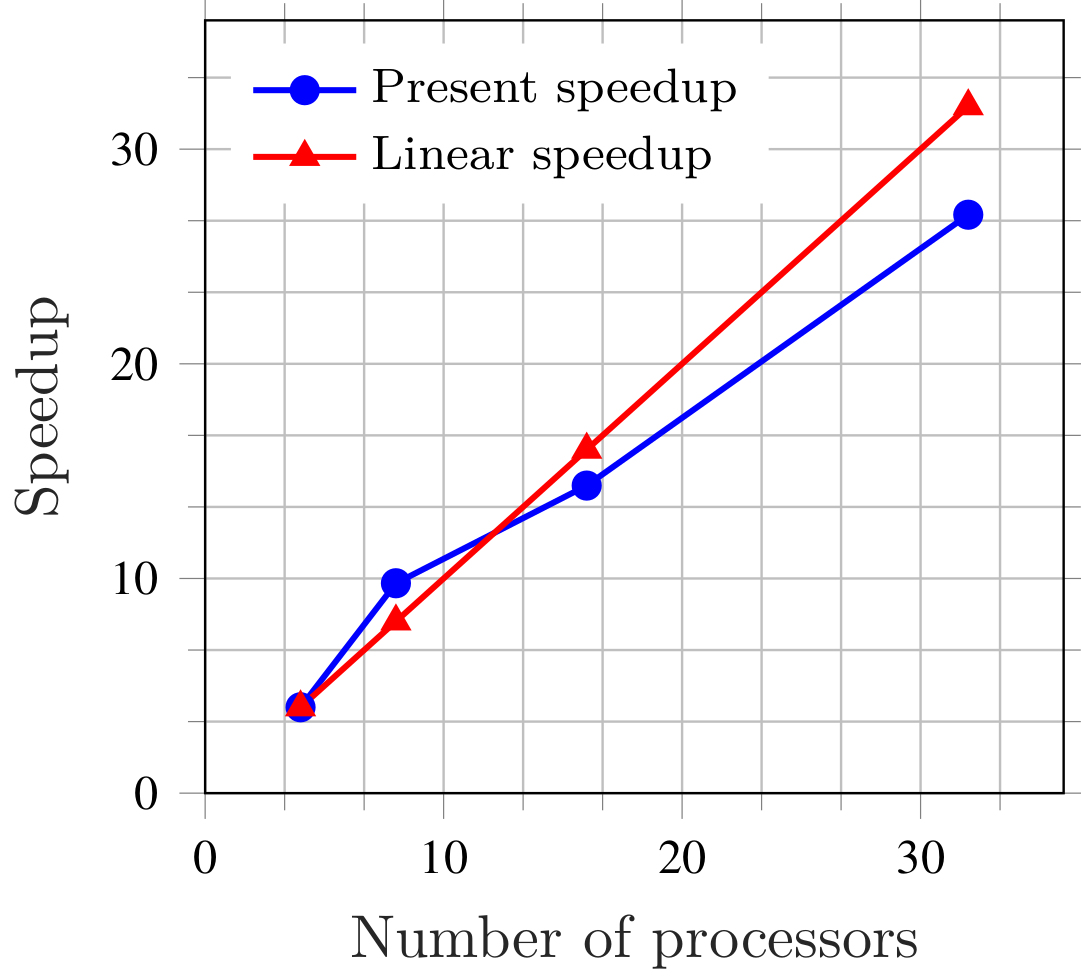
The in-house CFD code that we use to simulate fluid-structure interactions (FSI) has two crucial drawbacks: (a) it lacks the scalability required to perform large-scale simulations across several processors (CPUs), and (b) it has a severe computational bottleneck that deals with how the fluid and structural dynamics are coupled to each other. This bottleneck has not been addressed in literature. To tackle these issues, we have developed a scalable and efficient FSI algorithm using PETSc/MPI that employs a novel precomputable fluid-structure coupling strategy and leverages the parallel computing capabilities of supercomputers. More details about this work can be found [here].
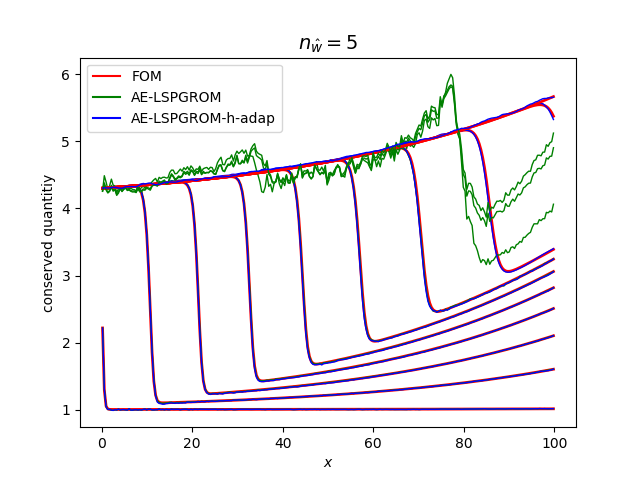
4. Guaranteeing convergence of reduced-order models (ROM) using transfer learning
Recently, deep convolutional autoencoders have been used to construct nonlinear manifolds for model order reduction. However, attaining guaranteed convergence of these reduced-order models, specifically for future time predictions, has been a significant challenge due to the nonlinear nature of the manifold. In this project, we worked on developing an adaptive manifold refinement strategy wherein (a) the basis (or the first fully connected layer) of the latent space of the decoder was split to form a larger subspace and (b) few selected weights of the decoder neural network were retrained efficiently. By adaptively increasing the latent space basis and the number of weights trained for transfer learning, convergence of the nonlinear ROM was expected. This approach was tested on a one-dimensional Burgers equation involving a traveling shock wave.
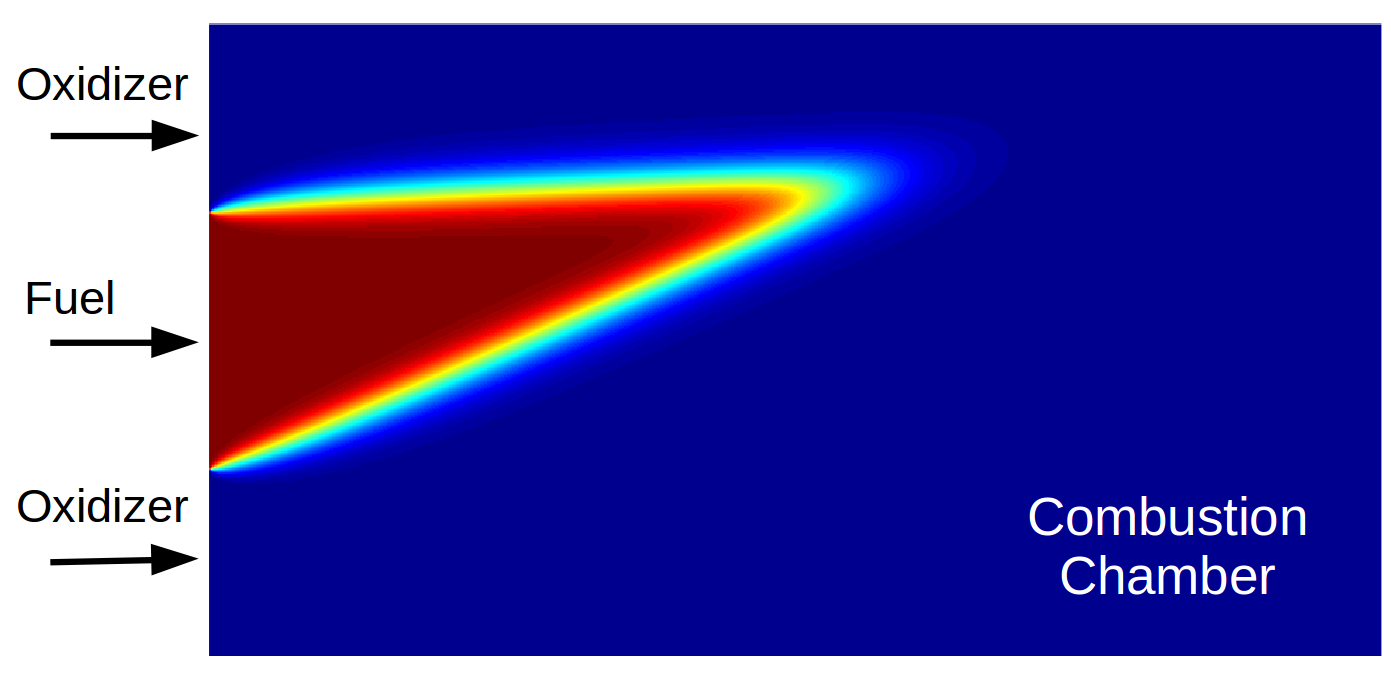
5. Data-driven reduced order modeling of fluid flows
Traditional ROM approaches cannot be expected to efficiently provide good approximations in the case where the solutions are dominated by strong shocks or discontinuities whose spatial orientations and positions are strongly parameter dependent. To tackle this problem, we developed a model order reduction method where nonlinear transformation of a linear subspace is performed by transporting few selected snapshots in parameter space based on precomputed transport velocities. We demonstrated the accuracy and computational efficiency of our approach on many representative flow problems such as a supersonic two-dimensional flow over a forward facing step resulting in multiple shock interactions and reflections and a multi-parametric combustion problem. More details about this work can be found [here].

Selected Course Projects
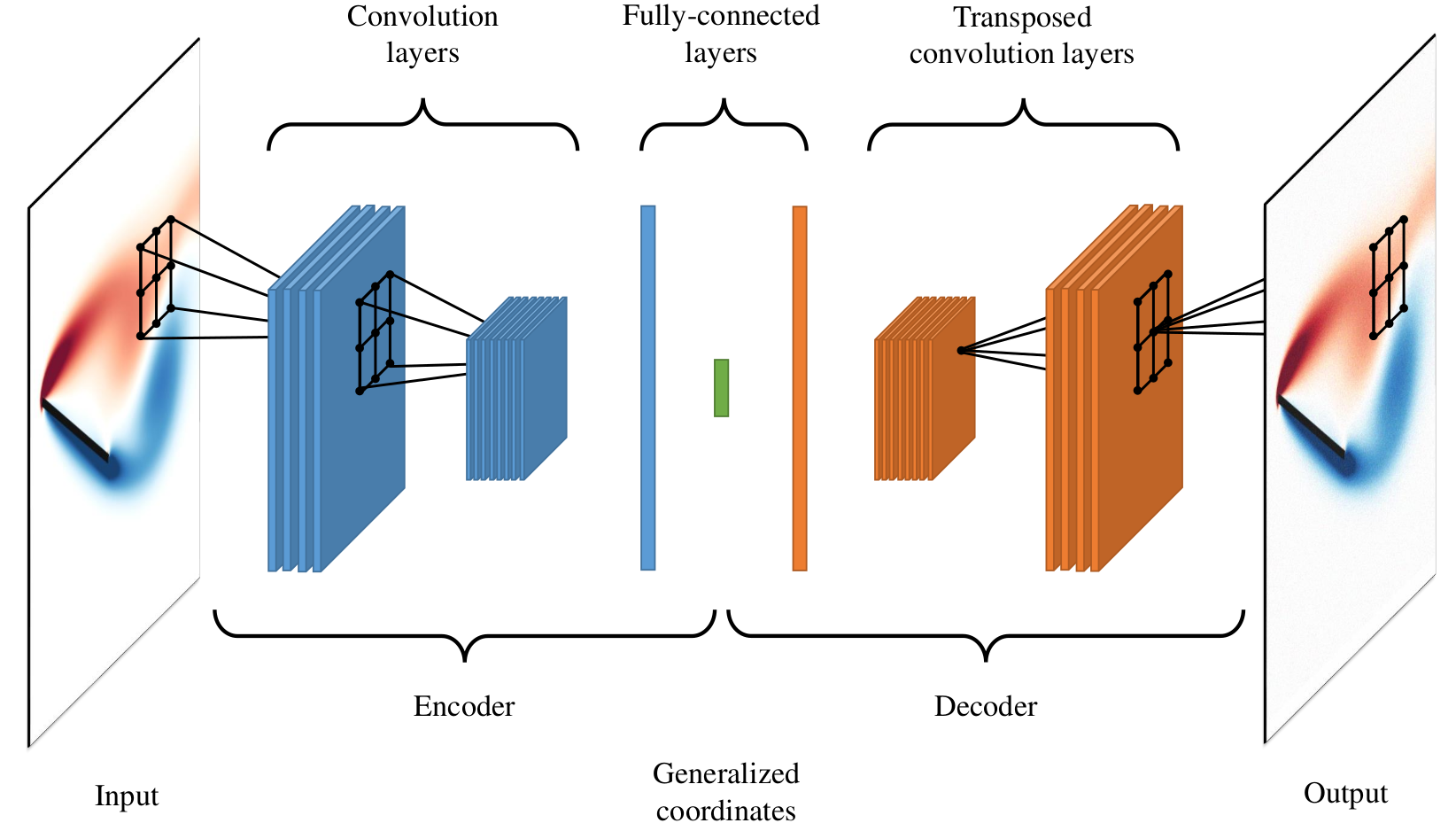
1. Pattern recognition in fluid dynamics using deep convolutional autoencoders
We developed a nonlinear modal decomposition framework for accurately representing transient fluid flows where traditional techniques perform poorly. In this approach, the flow patterns identified by the manifold were analyzed by evaluating the principle directions of the low-dimensional latent space. The nonlinear manifold was constructed using a deep convolutional autoencoder. The proposed framework was demonstrated to reconstruct and identify dominant and meaningful flow patterns in a transient flow ensuing from an impulsive motion of a flat plate at a large angle of attack.
2. Aeroacoustics of vortex shedding about a stalled airfoil
The Ffowcs Williams-Hawkings (FWH) equation for predicting acoustic pressure was numerically solved using the Farassat Formulation 1A. This formulation has been historically used for predicting helicoptor rotor and propeller noise. First, the code was validated against analytical solutions consisting of stationary and moving monopoles. The validated code was then used to predict vortex shedding noise about a stalled airfoil.

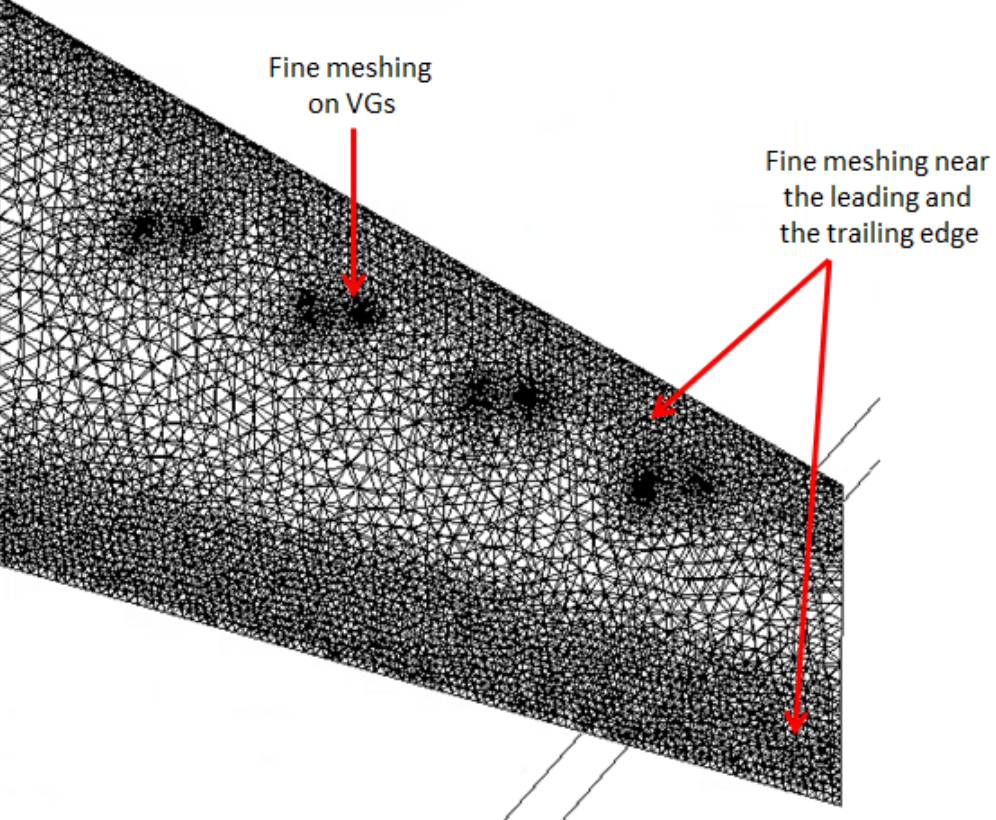
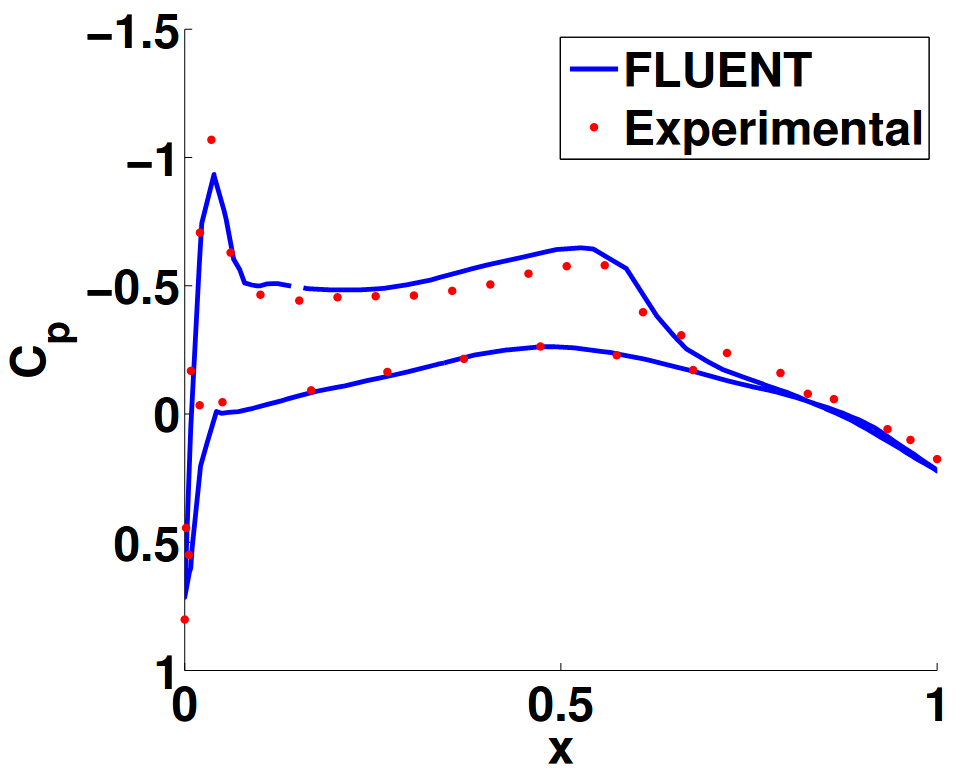
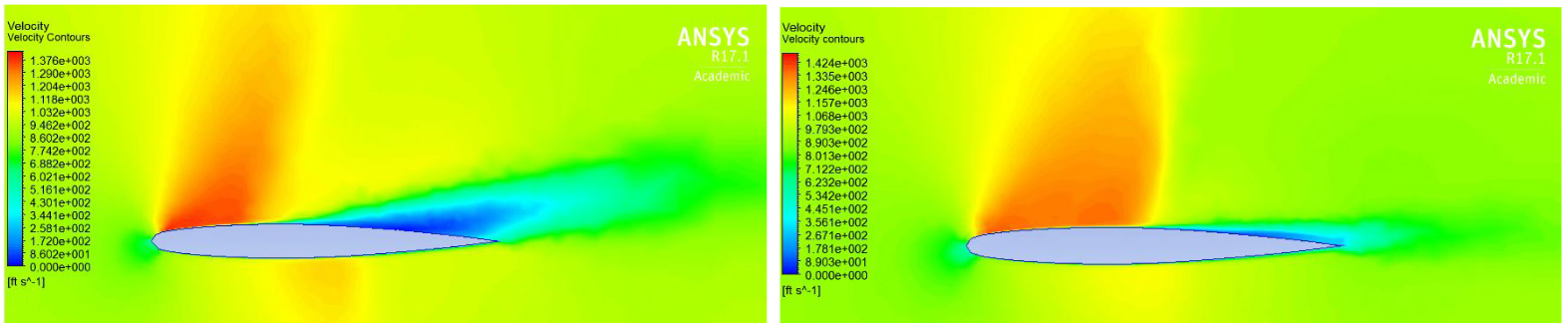
3. Shock induced flow separation control using vortex generators
Shock induced flow separation during transonic flow conditions decreases the aerodynamic performance of the wing. In this work, passive flow control of transonic flow past an Onera M6 wing using vortex generators was studied. The CFD simulations were performed on Ansys Fluent. Velocity contours at various spanwise locations revealed the delay of shock occurrence downstream and reduced flow separation. The resulting improvements in the lift to drag ratio, implied that the vortex generators improved the aerodynamic performance of the wing.